Съвременният анализ на времеви редове разчита на статистически модели, които улавят различни закономерности в данните. Два мощни модела, използвани във финансите и икономическото прогнозиране, са:
- ARIMA модели → фокусирани върху средната стойност, т.е. моделиране на предсказуемата част от доходността.
- ARCH модели → фокусирани върху волатилността, т.е. моделиране на изменчивостта на доходността (вариацията).
В тази статия ще разгледаме:
- Общата концепция на ARIMA моделите и техните разновидности.
- Общата концепция на ARCH моделите и техните разновидности.
- Основни понятия като стационарност и сезонност.
- Прости Python примери.
Какво са стационарни и сезонни данни?
- Стационарни данни са такива, при които средната стойност и вариацията остават постоянни във времето. Те нямат траен тренд или повтарящи се модели. Много статистически модели, например ARIMA, изискват данните да са стационарни.
- Сезонни данни показват редовни, повтарящи се модели през определени интервали (напр. месеци, тримесечия). Пример: продажбите на сладолед са високи всяко лято.
Когато имаме сезонност, данните често не са стационарни. За да ги моделираме правилно, премахваме сезонните ефекти (напр. чрез сезонно диференциране или използване на модели като SARIMA).
Обща концепция на ARIMA моделите и техните разновидности
Какво е ARIMA?
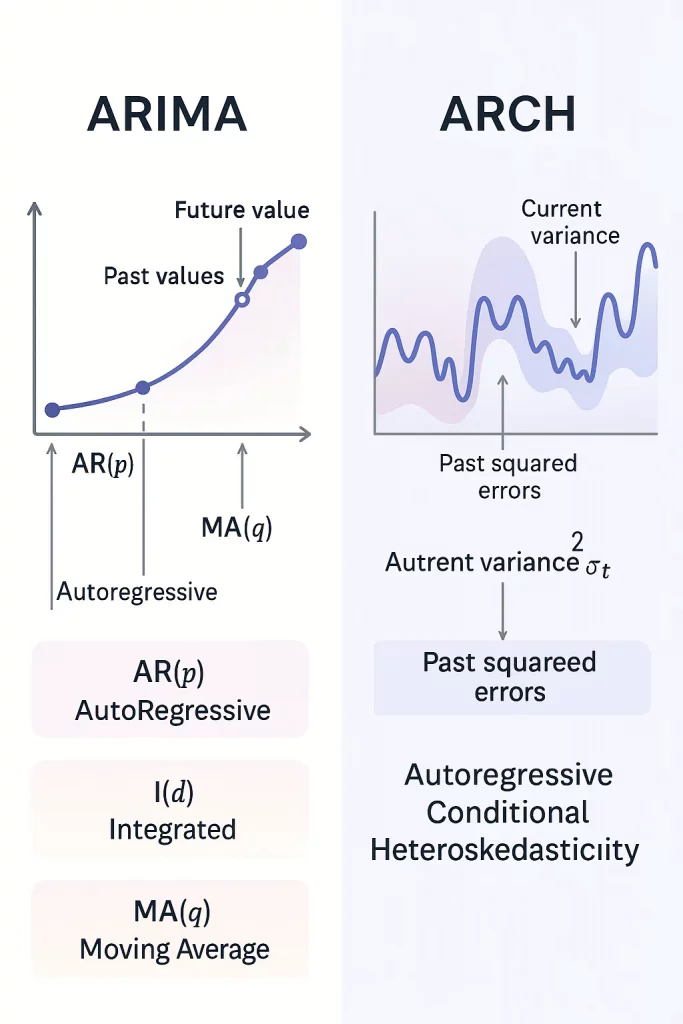
ARIMA означава:
- Авторегресивен (AR) – редицата зависи от собствените си предходни стойности.
- Интегриран (I) – прилага се диференциране, за да стане редицата стационарна (т.е. със стабилна средна стойност и вариация във времето).
- Подвижна средна (MA) – редицата зависи от минали стойности на грешките (шумовете) от прогнозата.
ARIMA моделира средната стойност на времевата редица, като улавя:
✅ Корелационни зависимости в доходността (напр. минали доходности предсказват бъдещи)
✅ Корелационни зависимости в остатъците (грешките също могат да показват закономерности)
✅ Няма сезонност при обикновения ARIMA.
✅ Данните трябва да са стационарни.
SARIMA: Добавяне на сезонност
Когато данните имат ясно изразена сезонност, ARIMA се разширява до SARIMA (Seasonal ARIMA), която добавя сезонни компоненти, за да улови тези повтарящи се модели.
Пример с ARIMA в Python

Обща концепция на ARCH моделите и техните разновидности
Какво е ARCH?
ARCH означава:
- Авторегресивен (AR) – редицата зависи от собствените си предходни стойности.
- Условен (C) – дисперсията (волатилността) се променя в зависимост от наличната информация от предходни периоди.
- Хетероскедастичност (H) – дисперсията не е постоянна във времето.
Докато ARIMA моделира средната стойност на времевата редица, ARCH моделира волатилността на остатъчните стойности (грешките), които остават след прилагането на ARIMA модела.
ARCH улавя:
✅ Хетероскедастичност → вариацията не е постоянна във времето.
✅ Клъстериране на волатилността – периоди на висока волатилност следват висока волатилност.
Много полезно за финансови данни, където волатилността се мени.
Разширения на модела
GARCH (Генерализиран Авторегресивен Условен Хетероскедастичен модел)
GARCH разширява ARCH модела, като позволява текущата волатилност да зависи не само от минали квадратични грешки (ARCH ефект), но и от собствените си предходни стойности (GARCH ефект).
Това води до по-гъвкаво и реалистично моделиране на динамиката на волатилността, особено при финансови времеви редици.
TARCH (Прагов Авторегресивен Условен Хетероскедастичен модел)
TARCH въвежда асиметрия в моделирането на волатилността, като позволява негативните шокове (лоши новини) да имат по-голямо въздействие върху бъдещата волатилност в сравнение с позитивните шокове със същата сила.
Това помага да се улови така нареченият лостов ефект (leverage effect), често наблюдаван на финансовите пазари.
Пример с GARCH в Python

ARIMA и ARCH – Накратко
- ARIMA → Средна стойност
- Моделира автокорелацията в редицата.
- Предполага постоянна волатилност (ако не се комбинира с ARCH).
- Няма сезонност, освен при SARIMA.
- Данните трябва да са стационарни.
- ARCH → Волатилност
- Моделира хетероскедастичността.
- Улавя клъстерирането на волатилността.
- Полезен за анализ на риск и волатилност.
Обикновено се комбинират:
- ARIMA за средната стойност.
- GARCH за волатилността на остатъците.
Заключение
Разбирането на ARIMA, SARIMA, ARCH, GARCH и TARCH ви помага да:
- Моделирате предсказуеми модели в данните (ARIMA/SARIMA).
- Анализирате и прогнозирате волатилността (ARCH/GARCH/TARCH).
Ако работите с икономически показатели или финансови данни, тези модели са основа за качествено прогнозиране.
Разберете повече за AIC и BIC: Избор на модел за прогнозиране на времеви серии.

