Heteroskedasticity vs. Homoskedasticity: What’s the difference and why does it matter?

For econometrics and regression analysis, heteroskedasticity and homoskedasticity are two fundamental concepts every data analyst needs to be aware of. Heteroskedasticity and Homoskedasticity explain the spread (or variation) of the errors (residuals) of a regression model. Both have critical roles to play in statistical inference validity, and understanding them is important in drawing valid conclusions from your data analysis.

Let’s find out what these words are, how to recognize them, and why they are important in statistical modeling.

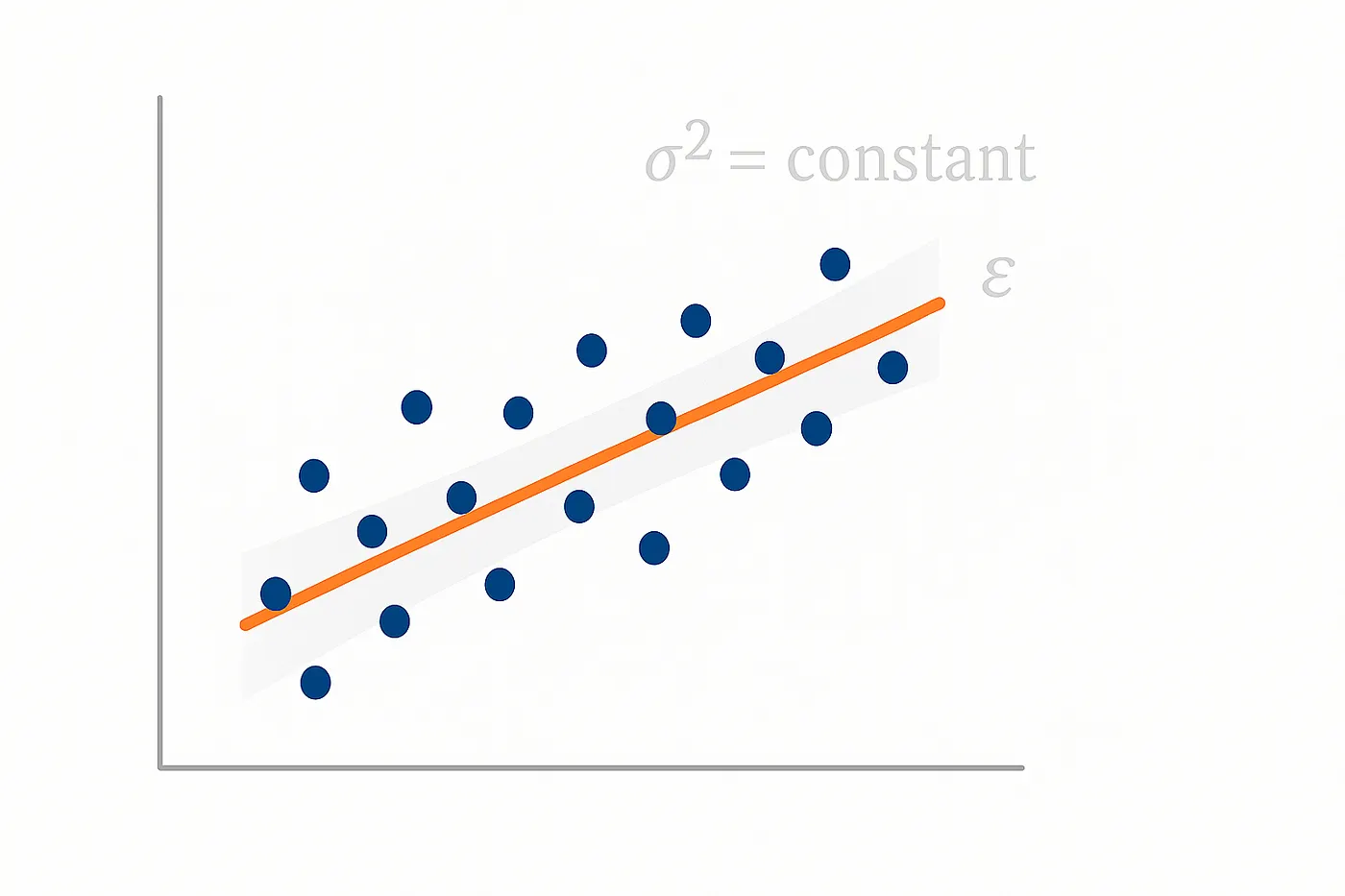
What is Homoskedasticity?

Homoskedasticity is a condition where the variance of the error (residuals) of a regression equation is constant across all levels of the independent variable(s). In other words, the variation of the residuals is the same regardless of the values of the independent variables. This assumption is required because, in the majority of statistical tests, we are assuming that the error terms are of a similar nature throughout the data.

Key characteristics of Homoskedasticity:

1. The variance of the residuals is constant for all observations.
2. The points are randomly scattered around the regression line, with no trend in the residuals.
3. Graphically, if you plot the residuals against the fitted values, the points should be randomly scattered, with no specific trend or shape.

In the utopian world of regression analysis, we would want homoskedasticity because it makes statistical tests and confidence intervals more accurate and trustworthy.

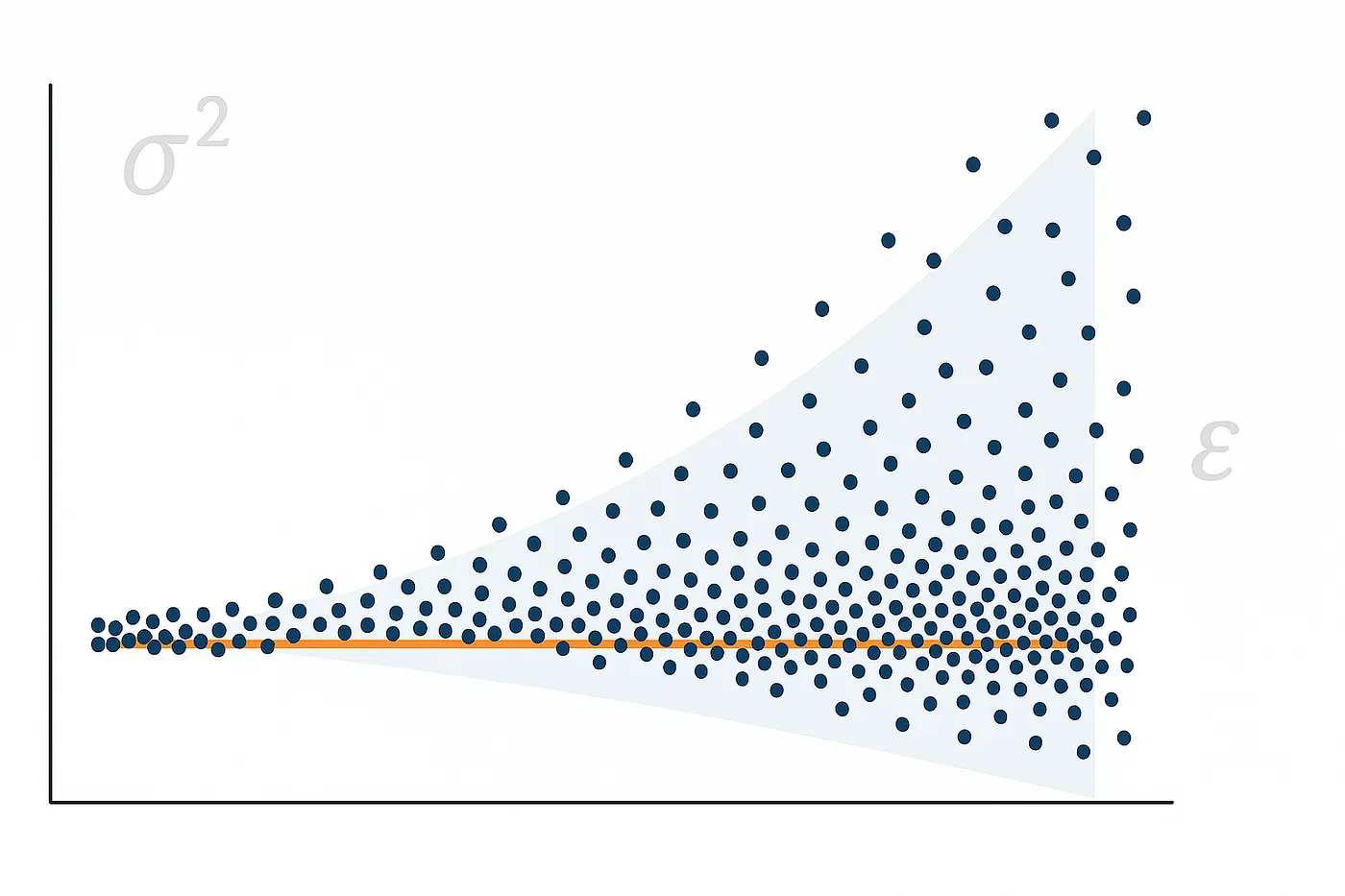
What is Heteroskedasticity?

Heteroskedasticity is the condition when error variance is not the same. In this case, the spread of residuals changes with changes in the independent variable(s) values. That is, the errors in certain measurements of the model would be large while others might be small.

Key characteristics of Heteroskedasticity:

1. The variance of the residuals changes with the independent variable(s) or the fitted value.
2. You might notice a pattern in the residuals, e.g., a funnel (where residuals increase as fitted values increase) or a “megaphone” shape.
3. Graphically, when residuals are plotted against fitted values, the points can be in a conical shape or a pattern where the spread is increasing or decreasing at different levels.

Heteroskedasticity has the potential to create inefficient estimates and bias the result of statistical tests, which will make it come to the wrong conclusion if not addressed well.

Why are Heteroskedasticity and Homoskedasticity important?

Homoskedasticity or heteroskedasticity signifies that the result of regression analysis is reliable or unreliable. The reasons are given as below:

1. Impacts on Ordinary Least Squares (OLS) estimates:

• Homoskedasticity: In case errors are homoskedastic, then the OLS would render the best, unbiased, and efficient estimates for the model parameters. Homoskedasticity satisfies one of the basic assumptions under which the OLS is BLUE (Best Linear Unbiased Estimator).
• Heteroskedasticity: OLS estimators are still unbiased if the errors are heteroskedastic, but are no longer efficient (they are no longer BLUE). The standard errors of the coefficients may be in error, resulting in biased t-tests and confidence intervals. Misestimated or overestimated, or underestimated significance levels, along with accompanying wrong conclusions, can occur.

2. Impact on Statistical Tests

• Homoskedasticity allows the standard errors of the regression coefficients to be consistent, and hypothesis tests (e.g., t-tests and F-tests) are valid.
• Heteroskedasticity may lead hypothesis tests to yield false conclusions. Under heteroskedasticity, standard errors may be biased, and hence significance tests (e.g., t-tests) are invalid.

3. Efficiency and Confidence Intervals

When heteroskedasticity is present, the efficiency of estimators is reduced, and confidence intervals expand beyond what they should be. This makes the estimates less accurate, which can negatively impact decision-making in business, economics, or whatever profession that relies on data analysis.

How to detect Heteroskedasticity

There are several methods for detecting heteroskedasticity within your data:

• Visual Inspection (Residual Plots):

The simplest way is to create a residual plot by plotting the residuals (errors) against the fitted values (predicted values). If the plot exhibits a pattern (such as a funnel shape), then it’s a sign of heteroskedasticity. We typically identify homoskedasticity by a random scatter of points.

• Breusch-Pagan Test:

This is a formal statistical test for heteroskedasticity. The test inspects whether or not the residual variance is related to the value of the independent variables.

• White’s Test:

Another statistical test can help determine whether heteroskedasticity is present. It is more flexible than the Breusch-Pagan test and does not depend on a specific functional form of heteroskedasticity.

This is useful when you suspect heteroskedasticity because of some particular variable (e.g., income or size) on which heteroskedasticity relies.

How to cure Heteroskedasticity

If we detect heteroskedasticity, we can address it in several ways:

1. Weighted Least Squares (WLS)
   WLS extends OLS by assigning different weights to observations. The method gives less weight to observations with larger error variance and more weight to those with smaller error variance. This can help in mitigating the effect of heteroskedasticity.
2. Robust Standard Errors
   You can use robust standard errors, which account for heteroskedasticity and make the estimation of standard errors more precise. This does not actually correct for the underlying heteroskedasticity in the data, but makes your statistical tests less vulnerable to it happening.
3. Transforming the Dependent Variable
   In certain situations, applying a transformation (e.g., log transformation) to the dependent variable will stabilize the variance and fix the heteroskedasticity.
4. Model Specification
   It might be worth reassessing your model. Heteroskedasticity may occasionally be the result of a misspecification of the model or an omission of important variables that must be in the model.
5. Box-Cox Transformation
   A more flexible approach that identifies the best power transformation for your data automatically, often effectively removing heteroskedasticity.

Having knowledge about the distinction between heteroskedasticity and homoskedasticity is important for accurate statistical analysis and decision-making. Homoskedasticity ensures constant residual variance and supports valid statistical inference. Heteroskedasticity, in contrast, can reduce the efficiency and accuracy of regression estimates and hypothesis tests.

When working with real data, it is good practice to test for heteroskedasticity. This is especially important if the error variance may vary across levels of the independent variable. If you do encounter heteroskedasticity, there are a number of means by which you can correct to make it away from, including with robust standard errors, weighted least squares, or data transformation.

By recognizing and addressing these issues, you can improve the precision of your regression models and make better decisions from your analysis.

Confidence interval: Why do we have outliers? How is this relevant to our assumptions?

Read here