In statistical analysis and modeling, awareness of confidence intervals and detection of outliers plays a significant role when making valid inferences from the data. Both bear an association with uncertainty but provide different information about what we currently know. In this, we will delve into what confidence intervals are, why and how outliers happen, and how they are both vital while making assumptions from your dataset.
What is a confidence interval?
A confidence interval (CI) is a range of values that we utilize to make an estimate of the population parameter’s actual value, say the mean or proportion. Rather than a point estimate, a confidence interval tells us an interval within which we can anticipate the actual value, with some level of confidence.
For example, suppose that a poll states that 65% prefer a candidate whose 95%-confidence interval is [60%, 70%], then what is true is that if one were to do the poll repeatedly many times, then 95% of times the true rate of support lies between 60% and 70%.
Confidence intervals are used most commonly in hypothesis testing, regression analysis, and population parameter estimation. Confidence intervals are used to express our uncertainty in a quantitative form and are generally expressed as a percentage (e.g., 95% or 99%).
How is confidence interval calculated?
The formula for a confidence interval typically relies on the type of data you are working with (e.g., mean, proportion). A general formula for the confidence interval of the mean, when the sample size is large and the standard deviation is known, is:
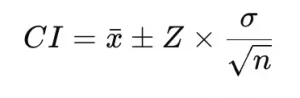
Where:
x̄ is the sample mean
Z is the Z-score corresponding to the confidence level (1.96 for 95% confidence)
σ is the population standard deviation
n is the sample size
For smaller sample sizes or when the population standard deviation is unknown, you might use the t-distribution to calculate the confidence interval
Why do we have outliers?
An outlier is a number that is extremely different from other observations in the data set. It can be significantly higher or significantly lower than the rest of the data. There are many reasons why outliers occur and they are categorized into two types:
- Natural Variation: Outliers can be just due to natural variation of the data. For example, if you were attempting to measure how tall a group of people are. Most would be around some mean, but one extremely short or extremely tall individual would be an outlier.
- Errors in Recording or Data Collection: Outliers are at times the outcome of errors, i.e., measurement errors, entry errors, or reporting errors. These would generally be trapped and corrected or removed during data cleaning.
Outliers may occur for a variety of reasons, and knowing whether they represent good data points or not is important. Whether to retain or delete outliers is a function of the context of your analysis and the particular assumptions you’re making about your data.
Why are outliers important in confidence intervals?
Outliers are extremely crucial in statistical analysis because they can skew your results and affect the validity of your confidence intervals. This is how outliers impact your confidence interval:
- Increase in Range: Outliers will make the width of a confidence interval wider, lessening its accuracy. For example, an extremely high or extremely low value may draw the mean towards it, making the range of the confidence interval wider and hopefully causing you to think the data is more uncertain than it actually is.
- Impact on Assumptions: Statistical analysis presupposes that data is normally distributed in most instances. Outliers may imply that data doesn’t align with this assumption, thereby rendering analysis results invalid. You might need to find out whether your data is normally distributed (using normality tests or plots like histograms) if you have outliers.
How do outliers impact assumptions
When you make assumptions about your data (for example, assuming it’s normally distributed), outliers will invalidate such assumptions. Here’s why:
- Violation of Normality Assumption: There are a number of tests that rely on the normality assumption of the data. Outliers would mean that data is heavy-tailed or skewed, hence the normality assumption is no longer valid. Then you may have to use non-parametric tests or transform your data (e.g., log-transformation) such that your tests’ assumptions are better satisfied.
- Inflation of Error Terms: Outliers can inflate the standard error, which is a crucial component when calculating confidence intervals. As you have larger error terms, your confidence interval is going to be larger, and therefore your estimate of your population parameter is less precise. Your conclusion is less accurate.
How to handle outliers in confidence intervals?
There are a couple of things you can do when dealing with outliers, especially when constructing confidence intervals:
- Use Stronger Methods: Stronger statistical methods are less influenced by outliers. For example, the use of the median instead of the mean for central tendency, or the application of robust standard errors minimizes the influence of outliers.
- Transform the Data: Sometimes, data transformation (e.g., log) can decrease the influence of outliers and spread the data in a more normal distribution, which can restore the validity of your assumptions.
- Investigate the Cause: If you discover the outlier to be the product of data collection or measuring error, you would then have to remove it after establishing that it was in error. But if it’s an actual observation, you might have to adjust your analysis to accommodate it.
- Consider the Context: It’s important to consider the context of your data before deciding how to treat outliers. For example, in financial markets, extreme outliers (like market crashes) might be important events that should not be removed.
Confidence intervals are a great way to communicate uncertainty in your statistical estimates but can be affected by outliers. Outliers can make your confidence intervals wider and less accurate. They can also break normality assumptions, leading to incorrect conclusions. In order to interpret your data correctly, it’s crucial to treat outliers with care and account for how they’ll affect your assumptions and results.
Understanding the role of outliers and how to process them allows more precise and meaningful statistical analysis, especially when processing confidence intervals.