Какво представлява разпределение на данни? Защо е важно в анализа на данни? Създайте своя първи PDF

Една от най-основополагащите идеи в науката за данните и анализите е разпределение на данни. Това е изключително важна концепция, която помага на анализаторите да разберат как са разпределени данните – знание, което влияе върху статистическия анализ, вземането на решения и прогностичното моделиране.

В тази блог статия ще обясним какво представлява разпределение на данни, защо е толкова важно и как да генерирате PDF (Probability Density Function — функция на плътността на вероятността) в Python.

Какво представлява разпределение на данни?

Разпределението на данните описва начина, по който стойностите в даден набор от данни са разпръснати или разпределени в определен диапазон. То представлява формата или структурата, която данните имат, когато бъдат визуализирани на графика. Разпределението ни дава ценна информация за структурата и закономерностите, които стоят зад набора от данни.

Съществуват много видове разпределения, използвани в статистиката, но най-разпознаваемите са:

1. Нормално разпределение: Наричано още Гаусово разпределение, това е едно от най-често използваните разпределения в статистиката. То е симетрично и има форма на камбановидна крива. Повечето природни явления (като ръст на хора, резултати от тестове и др.) следват нормално разпределение.

2. Равномерно разпределение: При този вид разпределение всички резултати са еднакво вероятни. То има плоска, равномерна структура на стойностите в дадения диапазон.

3. Експоненциално разпределение: Обикновено се използва за моделиране на времеви интервали между събития в процес на Поасон, например времето на изчакване между пристигането на автобуси.

4. Биномно разпределение: Използва се за данни, които имат два възможни резултата, например успех или провал. Среща се често в случаи с фиксиран брой опити и известна вероятност за успех.

Защо е важно при анализа на данни?

Разбирането на разпределението на данните е ключово, тъй като ни дава информация за общата структура, централната тенденция и вариацията в набора от данни. Ето защо това има значение:

1. Защо познаването на разпределението е важно:
   Когато знаем как е разпределен наборът от данни, можем да определим дали следва разпознаваем модел (например нормално или експоненциално разпределение). Това ни помага да изберем подходящите статистически тестове и методи за моделиране.
2. Откриване на аномалии (outliers):
   Някои разпределения, като нормалното, са силно чувствителни към екстремни стойности. Затова е важно те да бъдат идентифицирани и обработени, тъй като могат да изкривят резултатите и да доведат до неточни заключения.
3. Избор на статистически техники:
   Различните разпределения изискват различни статистически методи. Например, ако данните са нормално разпределени, могат да се използват стандартни параметрични тестове (като t-тест). Ако данните не са нормално разпределени, по-подходящи са непараметрични методи (например тестът на Ман–Уитни U).
4. Предиктивно моделиране:
   При модели за машинно обучение разпределението на данните често определя кои алгоритми ще бъдат най-ефективни. Например линейната регресия работи най-добре с нормално разпределени данни, докато алгоритми като Random Forest могат да се справят добре и без строго разпределение.

Какво представлява функцията на плътността на вероятността (PDF)?

Функцията на плътността на вероятността (PDF) е статистическа функция, която описва вероятността непрекъсната случайна променлива да приеме дадена стойност. При непрекъснатите разпределения вероятността променливата да има точно определена стойност е математически равна на нула, но PDF позволява да изчислим вероятността стойността да попадне в определен интервал.

Накратко, PDF помага да визуализираме разпределението на данните и предоставя инструмент за изчисляване на вероятности. Площта под кривата на PDF представлява общата вероятност и тя винаги трябва да бъде равна на 1.

Създаване на PDF в Python

След като вече имаме представа какво са PDF и разпределението на данните, нека генерираме PDF в Python. Ще създадем базова крива на нормално разпределение и ще я визуализираме, използвайки библиотеки като NumPy и Matplotlib.

Създаване на PDF на нормално разпределение:

import numpy as np
import matplotlib.pyplot as plt

# Set mean (mu) and standard deviation (sigma)
mu, sigma = 0, 0.1
# Generate random data
data = np.random.normal(mu, sigma, 1000)

# Create histogram of the data
plt.hist(data, bins=30, density=True, alpha=0.6, color='g')

plt.title('Histogram of Normal Distribution')
plt.xlabel('Data Values')
plt.ylabel('Probability Density')

plt.show()

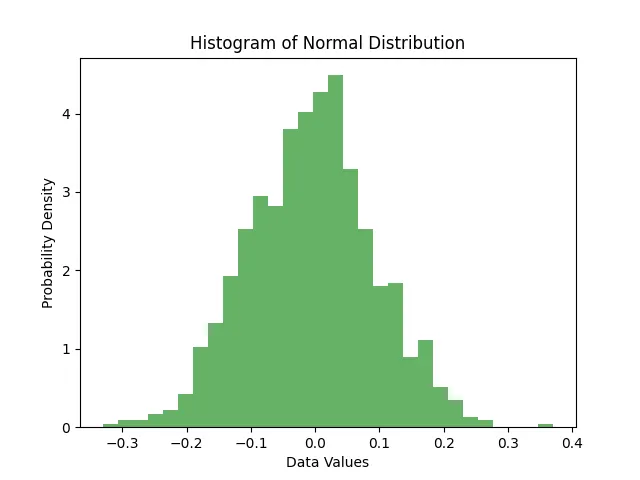
Създаване на PDF кривата

Сега нека изчислим функцията на плътността на вероятността (PDF) за нормалното разпределение и да я наложим върху хистограмата.

from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt

# Example data
data = np.random.normal(loc=0, scale=1, size=1000)
mu, sigma = np.mean(data), np.std(data)

# Plot histogram first
plt.hist(data, bins=30, density=True, alpha=0.6, color='b')

# Get the actual x-limits after histogram is drawn
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, mu, sigma)

# Plot the PDF
plt.plot(x, p, 'k', linewidth=2)
plt.title('Histogram and PDF of Normal Distribution')
plt.xlabel('Data Value')
plt.ylabel('Probability Density')
plt.show()

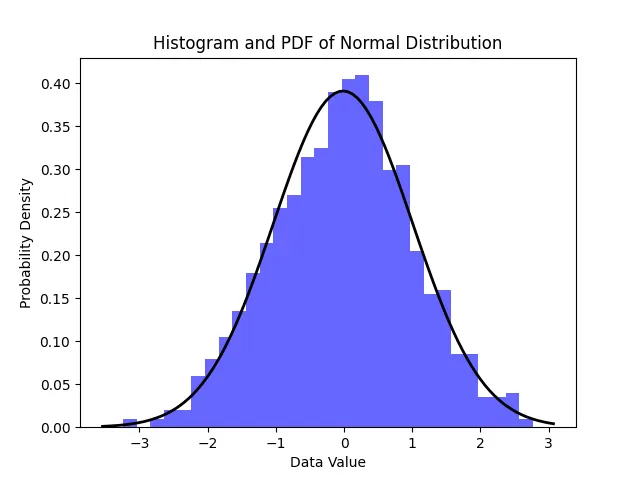
Хистограма с PDF графика

Разбирането на разпределението на данните е един от основните стълбове в анализа на данни. То ви позволява да разберете вашите данни, да идентифицирате тенденции, отклонения и да вземате информирани решения относно поведението на данните. В този материал разгледахме основите на разпределенията на данни, значението на PDF във анализа и дори създадохме проста PDF функция на нормално разпределение в Python.

За анализаторите и учените в областта на данните е ключово да визуализират и анализират разпределенията на данните. С мощните библиотеки на Python можете лесно да създавате и визуализирате тези разпределения, които са от съществено значение за разбиране на скритите модели и тенденции във вашите данни.