За иконометрията и регресионния анализ, хетероскедастичност и хомоскедастичност са две фундаментални концепции, които всеки анализатор на данни трябва да познава. Те обясняват разсейването (или вариацията) на грешките в регресионен модел. И двете играят критична роля за валидността на статистическите изводи и разбирането им е важно за правилното интерпретиране на резултатите от анализа на данни.
Нека разберем какво означават тези термини, как да ги разпознаем и защо са важни при статистическото моделиране.
Какво е Хомоскедастичност?
Хомоскедастичността е състояние, при което вариацията на грешките (резидуалите) на регресионното уравнение е константен за всички нива на независимите променливи. С други думи, вариацията е една и съща, независимо от стойностите на независимите променливи. Това предположение е необходимо, защото в повечето статистически тестове се предполага, че грешките са от сходен характер във всички данни.
Основни характеристики на хомоскедастичността:
-
Отклоненията на грешките са еднакви за всички наблюдения.
-
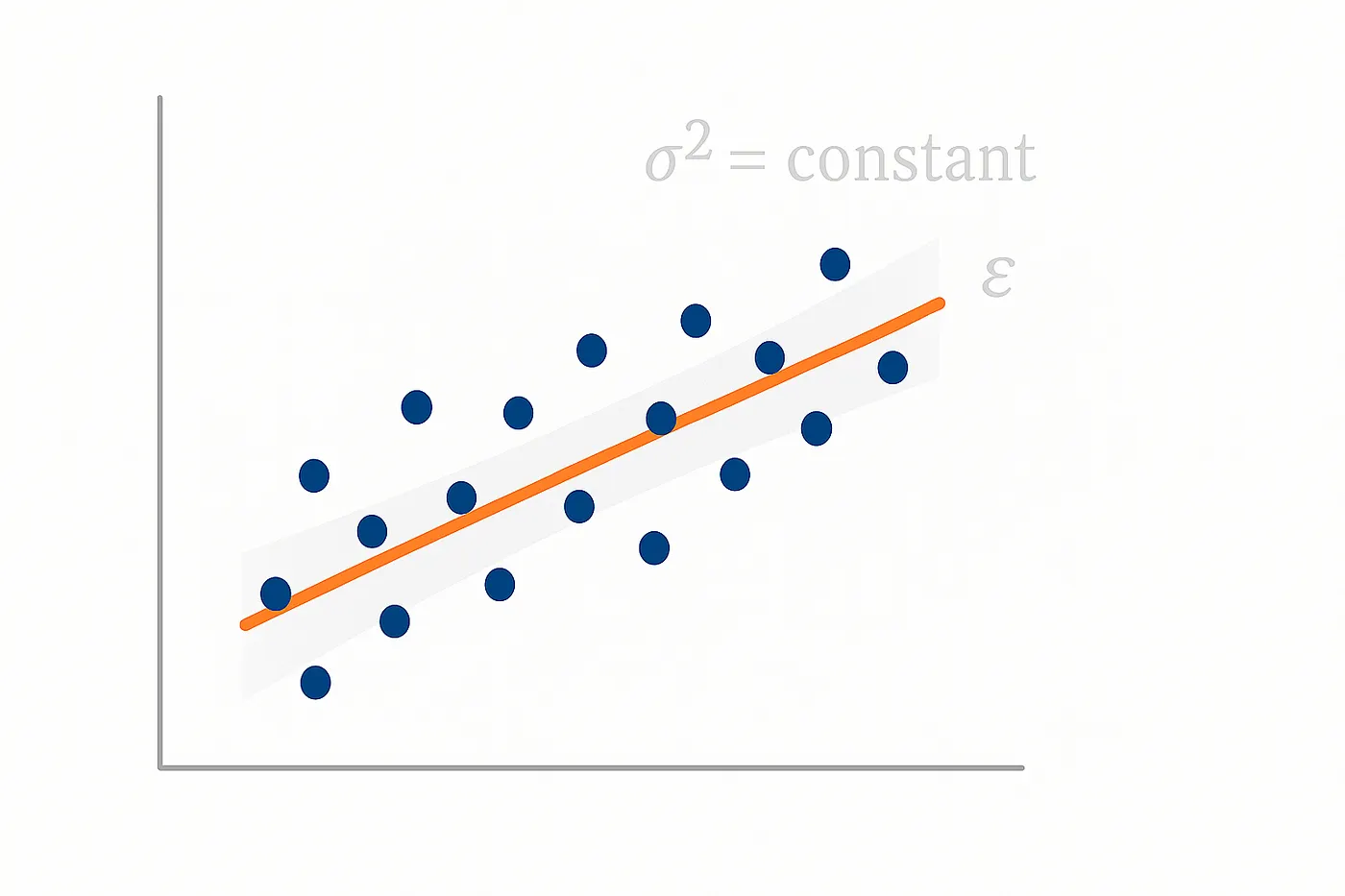
Точките са случайно разпръснати около регресионната линия, без видима тенденция в грешките.
-
Графично, ако начертаете грешките спрямо прогнозните стойности, точките трябва да са случайно разпръснати, без специфична форма или модел.
В идеалния свят на регресионния анализ хомоскедастичността е желана, защото прави статистическите тестове и доверителните интервали по-точни и надеждни.
Какво е хетероскедастичност?
Хетероскедастичност е състояние, при което отклоненията на грешките се променят. Това означава, че разсейването на грешките се увеличава или намалява в зависимост от стойностите на независимите променливи. Например, в някои наблюдения грешките могат да са големи, а в други – малки.
Основни характеристики на хетероскедастичността:
-
Отклоненията на грешките се променят спрямо независимите променливи или прогнозните стойности.
-
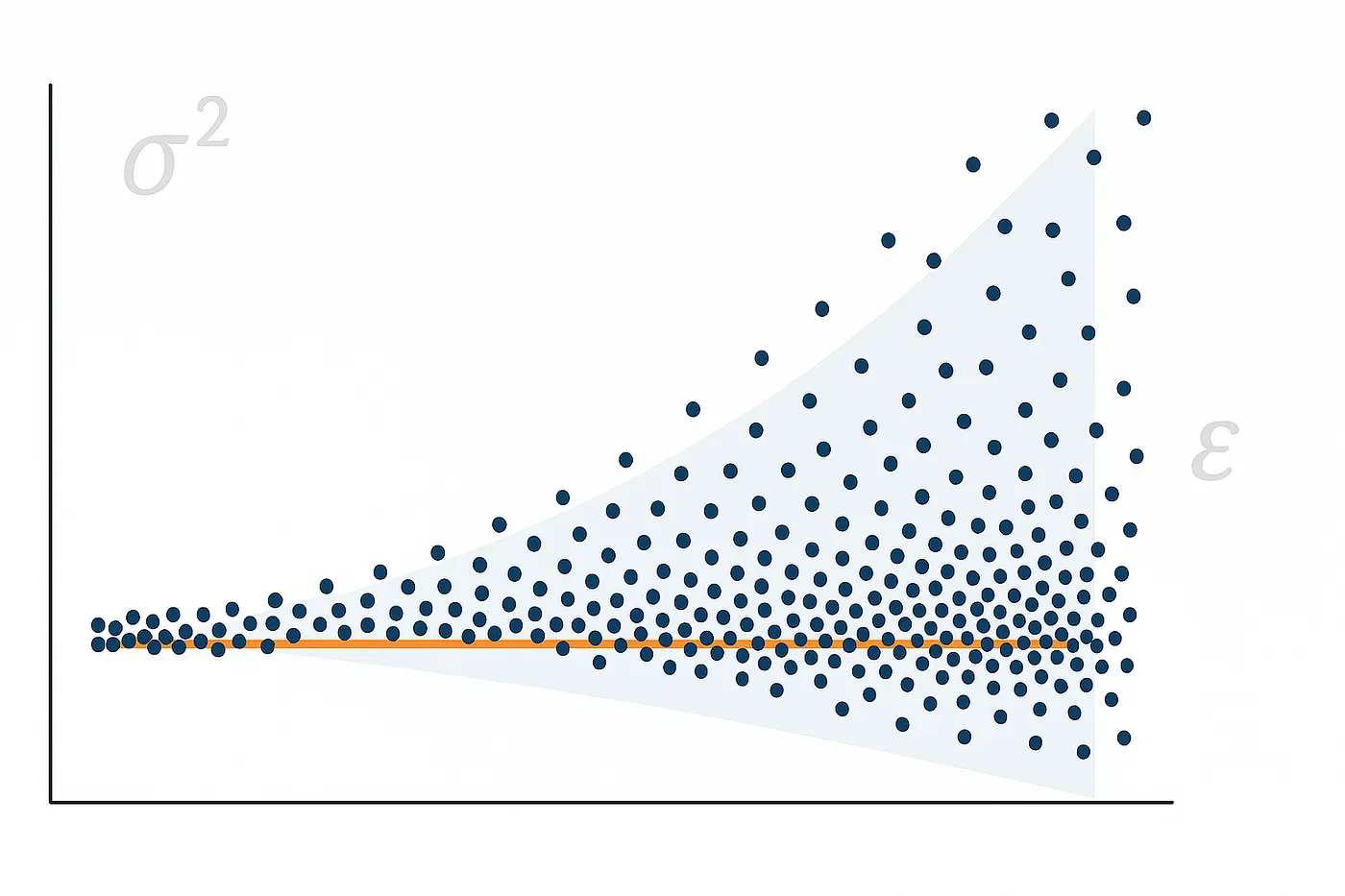
Може да се забележи определен модел в грешките, например форма на фуния (където грешките се увеличават с нарастване на прогнозните стойности) или „мегафон“.
-
Графично, точките могат да образуват конусна форма или модел, при който разсейването се увеличава или намалява на различни нива.
Хетероскедастичността може да доведе до неефективни оценки и да изкриви резултатите от статистическите тестове, което води до грешни изводи, ако не се коригира.
Защо хетероскедастичността и хомоскедастичността са важни?
Хомоскедастичността или хетероскедастичността показват дали резултатите от регресионния анализ са надеждни или не. Основните причини са:
1. Влияние върху оценките на OLS (Обикновени най-малки квадрати)
-
Хомоскедастичност: Ако грешките са хомоскедастични, OLS дава най-добрите, безпристрастни и ефективни оценки за параметрите на модела. Това удовлетворява едно от основните предположения, при които OLS е BLUE (Best Linear Unbiased Estimator – най-добър линейно безпристрастен оценител).
-
Хетероскедастичност: OLS оценките остават безпристрастни, но вече не са ефективни. Стандартните грешки на коефициентите могат да са неточни, което води до изкривени t-тестове и доверителни интервали. Това може да причини погрешно оценени или надценени/подценени нива на значимост и съответно грешни изводи.
2. Влияние върху статистическите тестове
-
Хомоскедастичност: Позволява стандартните грешки на регресионните коефициенти да са консистентни и хипотезните тестове (t-тестове, F-тестове) да са валидни.
-
Хетероскедастичност: Може да доведе до фалшиви изводи от тестовете. Стандартните грешки могат да са изкривени, което прави тестовете на значимост невалидни.
3. Ефективност и доверителни интервали
При наличие на хетероскедастичност ефективността на оценителите намалява, а доверителните интервали се разширяват. Това прави оценките по-малко точни и може да повлияе негативно на вземането на решения в бизнес, икономика или други професии, които разчитат на анализ на данни.
Как да открием хетероскедастичност
Визуална проверка (Residual Plots):
Най-простият начин е да се създаде графика на грешките спрямо прогнозните стойности. Ако се забелязва определен модел (например фуния), това е знак за хетероскедастичност. Хомоскедастичността се разпознава чрез случайно разпръснати точки.
Breusch-Pagan тест:
Формален статистически тест, който проверява дали разсейването на грешките е свързано със стойностите на независимите променливи.
White’s тест:
Друг статистически тест, който определя дали има хетероскедастичност. По-гъвкав е от Breusch-Pagan теста и не зависи от конкретна форма на хетероскедастичността.
Полезен е, когато хетероскедастичността зависи от конкретна променлива (например доход или размер).
Как да коригираме хетероскедастичността
Weighted Least Squares (WLS):
WLS дава различни тежести на наблюденията – по-малка тежест на грешки с голямо разсейване и по-голяма на тези с малко разсейване. Това намалява ефекта на хетероскедастичността.
Robust Standard Errors:
Използването на робустни стандартни грешки отчита хетероскедастичността и прави тестовете по-надеждни, без да премахва самата хетероскедастичност.
Трансформация на зависимата променлива:
Прилагането на логаритмична или друга трансформация на зависимата променлива може да стабилизира вариацията и да премахне хетероскедастичността.
Спецификация на модела:
Хетероскедастичността понякога се дължи на пропуснати важни променливи или неправилно зададен модел.
Box-Cox трансформация:
Автоматично намира най-подходящата степенна трансформация, която ефективно премахва хетероскедастичността.
Разбирането на разликата между хетероскедастичност и хомоскедастичност е важно за точен статистически анализ и информирано вземане на решения. Хомоскедастичността осигурява постоянни грешки и подкрепя валидни статистически изводи, докато хетероскедастичността може да намали точността и ефективността на регресионните оценки и тестове.
При работа с реални данни е добра практика да се тества за хетероскедастичност. Ако я откриете, има различни начини за корекция – робустни стандартни грешки, WLS или трансформация на данните.
Разпознавайки и коригирайки тези проблеми, можете да подобрите точността на моделите си и да вземате по-добри решения въз основа на анализа на данни.

