Преди да създадете печеливша стратегия за търговия, прогнозиране или обработка на сигнали, е важно да разберете характера на времевата редица. Тя може да е склонна към възвръщане към средната стойност, случайно движение или следване на тренд. Един от най-ефективните инструменти за това е експонентът на Хърст (H). Това е статистическа формула, кръстена на британския хидролог Харолд Едуин Хърст. Тя измерва дългосрочната памет на времевите редици. Затова е безценен инструмент за трейдъри, анализатори и изследователи.
Какво е средно стойностно възстановяване (Mean Reversion)?
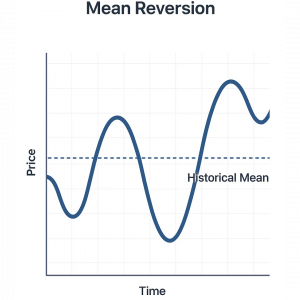
Връщането към средната стойност описва схващането, че дадена променлива ще се върне към историческата си средна стойност в дългосрочен план. Това може да е цена на акция, лихвен процент или валутен курс. Тази статистическа характеристика предполага, че много големи движения в една посока често са последвани от връщане към средната стойност. Така се създават възможности за печалба от временни неправилни цени на финансовите пазари.
На финансовите пазари, стратегиите на търговците , които са базирани на “mean reversion”, включват купуване на активи, когато цените им са ниски, и продаване, когато са високи. Идеята е, че цените в крайна сметка ще се върнат към своето средно ниво. Но не всички активи се държат така, затова е полезно да знаем дали една цена има склонност да се връща към средното ниво. Тук влиза в действие експонентът на Хърст – той помага да се определи дали даден актив обикновено се връща към средното, следва тенденция или се движи на случаен принцип.
Какво представлява експонентът на Хърст?
Експонентът на Хърст е също мярка за дългосрочна статистическа зависимост на данните от времеви серии. Той описва поведението на сериите по следния начин:
- H < 0,5: Времевите серии показват отрицателна зависимост между стойностите си във времето и се връщат към средната си стойност. Спадът става все по-вероятен след увеличение и обратно.
- H = 0,5: Времевите серии се държат като геометрично Брауново движение (или случайно блуждаене) и не показват предсказуемост или зависимост между стойностите във времето.
- H > 0,5: Времевите серии са устойчиви или с изразена тенденция и показват положителна времева зависимост – движението в една посока е по-вероятно да продължи, отколкото да се обърне..
Защо дългосрочната памет на времеви редици е важна?
Времевите редици с дълга памет не „забравят“ миналите си стойности – те продължават да оказват влияние в бъдеще. Това е противоположно на случайните процеси.
- Сериите с характеристики за връщане към средната стойност имат склонност да се движат в противоположна посока на предходното изменение – ако днес има ръст, утре има повишена вероятност за спад.
- Наличието на дългосрочна памет означава, че миналите стойности оказват влияние върху бъдещите, което позволява разработване на предсказуеми модели и стратегии.
- Силното средно стойностно възстановяване може да е индикатор за неефективности на пазара, които опитни трейдъри могат да използват.
Приложения на Хърст експонента във финансовата търговия
- Търговия по двойки (Pairs Trading): Hurst експонентът (H < 0.5) може да помогне за откриване на двойки активи със спред, който има склонност да се връща към средната стойност – индикация за потенциално средно-стойностно поведение.
- Статистически арбитраж: Чрез анализ на комбинации от активи с коинтеграция и характеристики на връщане към средната стойност (често свързани с ниски стойности на Hurst), експонентът подпомага разпознаването на дългосрочни равновесни зависимости.
- Стратегии за волатилност: Hurst експонентът може да подскаже кога волатилността има вероятност да се върне към нормални нива. Това може да се използва за откриване на потенциални възможности за дълги или къси позиции в активи, свързани с волатилността.
Предимства от използването на Хърст експонент
- Показва степента на предвидимост във времеви ред
- Помага да се идентифицират трендови поведения
- Подобрява оценката на риска, като разкрива случаи, в които предположенията за случайност може да са подвеждащи
Заключение
Експонентът на Хърст предоставя математически обоснован начин за оценка на потенциала за връщане към средната стойност във времевите серии. Независимо дали се използва при изграждането на алгоритмични търговски стратегии, при финансов анализ или за по-добро разбиране на пазарната динамика, анализът чрез Хърст допринася за по-задълбочено разбиране на дългосрочната зависимост в данните.
Добре разработеният подход за връщане към средната стойност, основан на анализа на експонентата на Хърст и подкрепен от статистическа проверка, може да бъде източник на постоянна възвръщаемост и надеждно допълнение към диверсифицирано търговско портфолио.

