Разбирането на пазарния сентимент винаги е било ключова част от финансовия анализ. Традиционно анализаторите се опират основно на сурови данни за цени и обеми, за да определят преобладаващото настроение на пазара. Въпреки това, в крипто пространството, където малките тенденции се променят бързо, а поведението на инвеститорите е силно реактивно, традиционните количествени методи често не успяват да уловят пълната картина.
Крипто пазарът е дълбоко свързан с бързо движещи се информационни потоци. Новини, съобщения, активност в социалните мрежи и геополитически събития могат да влияят на сентимента за минути. Това повдига важен въпрос:
Следва ли да измерваме пазарния сентимент директно от новинарските потоци, вместо да разчитаме само на пазарни данни?
Проблемът
1. Човешка природа
Инвестиционните решения се влияят от когнитивни пристрастия и емоционални реакции – основен принцип на поведенческите финанси. На пазари с бърза информационна обмяна, като крипто, тези емоционални реакции често усилват ценовите движения. Колкото повече участници реагират по сходен начин, толкова повече тяхното колективно поведение влияе директно на новините в крипто пазара.
2. Спекулации и информационен поток
Спекулативни новини, слухове и непроверени твърдения могат да предизвикат забележими промени в цените на крипто активите.
Днес информацията се разпространява по-бързо от всякога чрез социални мрежи, платформи за съобщения и онлайн общности. Въпреки че не всеки индивид може да движи пазара, източници с голям обсег или координирани вълни от сентимент могат значително да влияят върху краткосрочната ценова динамика. Регулаторният надзор в тази област все още се развива, което означава, че волатилността, задвижвана от сентимент, остава често срещана.
3. Геополитически и макроикономически фактори
Крипто пазарите, въпреки децентрализацията си, остават чувствителни към глобални макроикономически и геополитически събития. Съобщения за политики, регулаторни промени, въпроси на финансова стабилност или глобални конфликти многократно показват корелация с пазарния сентимент и волатилност. Стабилната макро среда обикновено подкрепя позитивен сентимент, докато несигурността може да предизвика спадове.
Тези фактори показват, че разчитането само на сурови ценови данни е недостатъчно. Пазарният сентимент се формира както от човешкото поведение, така и от новинарския поток, и и двете трябва да се вземат предвид.
Решението: Количествено измерване на новините в крипто пазара
За да оценим новинарския сентимент правилно, трябва да вземем предвид няколко ключови фактора:
1. Достоверност на източника
Не всички източници имат еднакво значение. Професионалните инвеститори често дават приоритет на реномирани финансови медии, институционални доклади или проверени съобщения.
Въпреки това социалните мрежи също играят роля като индикатор за сентимент, особено в крипто. Целта не е да ги игнорираме, а да претегляме източниците според тяхната надеждност.
2. Географски и икономически произход
Влиянието на новините често зависи от тяхното географско и икономическо произход.
Съобщения от големи икономики или ключови регулаторни органи (например САЩ, ЕС, Китай) обикновено имат по-широк ефект.
За разлика от тях, новини, свързани с по-малки пазари, могат да влияят само върху локални региони или конкретни проекти. Правилният модел за сентимент трябва да отчита това.
3. Авторитет на автора/публикуващата страна
Някои автори, анализатори и институции разполагат с исторически надеждна информация или по-близък достъп до индустрията. Други публикуват спекулативно или нискокачествено съдържание. Поради това количественото измерване на сентимента трябва да включва оценка за надеждността на автора.
4. Обхват и релевантност
Не всяка новина влияе на целия пазар:
-
Ъпдейт на протокола може да повлияе само на свързания с него токен.
-
Глобално регулаторно съобщение може да промени сентимента в целия пазар.
-
Съдебен иск или проблем с борса може да засегне конкретни сектори.
5. Потенциален пазарен ефект
Дори силният сентимент в една област не влияе непременно на по-широките пазарни тенденции. Моделът трябва да прецени дали новината има потенциално въздействие върху пазара или е изолирана само до конкретен актив.
Правилата: Построяване на количествена скала за сентимент
За да класифицираме сентимента на новините надеждно, дефинираме набор от правила.
Всяко правило оценява едно измерение (например качество на източника, релевантност, обхват на въздействие) и дава цяло число като резултат.
Всички резултати от правилата се комбинират в един нормализиран сентимент скор в зададен диапазон:
−100 = Много мечи
−50 = Мечи
0 = Неутрален
+50 = Бичи
+100 = Много бичи
Нормализацията гарантира, че системата за оценка никога няма да изведе стойности извън определените категории на сентимента.
Въпросът: Колко силен е сентиментът?
Когато приключим с дефинирането на правилата, трябва да вземем предвид разстоянието между изчислената стойност и прага на категорията.
Пример:
Ако Neutral = 0 и Bullish = +50, резултат от +25 е точно по средата между двете.
Но какво означава „наполовина бичи“ в количествено изражение?
Тук разграничаваме два сценария:
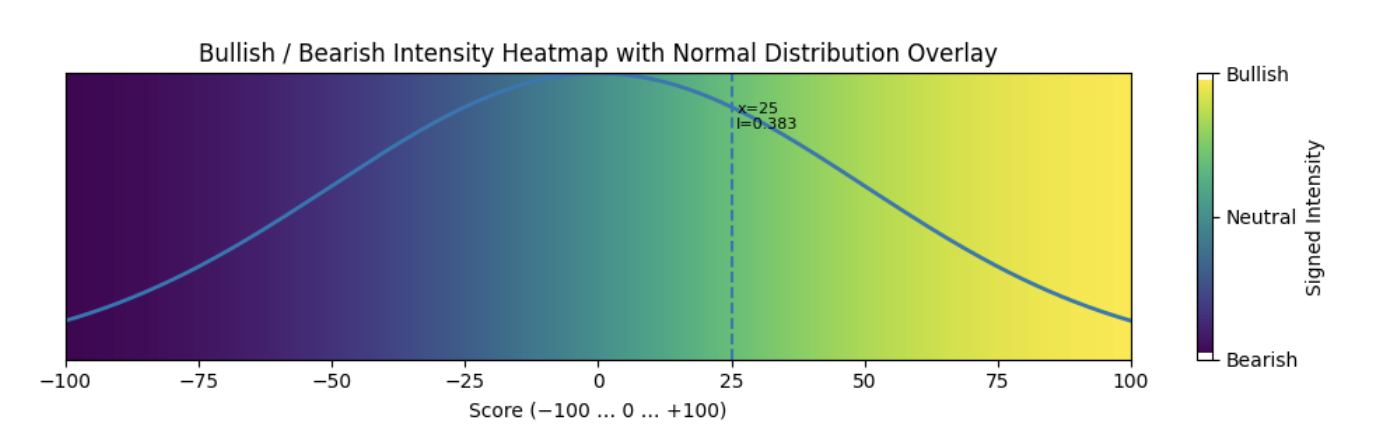
Сценарий 1: Малко новинарски данни (предполагаемо разпределение)
Когато липсват достатъчно наблюдения, приемаме, че резултатите следват приблизително нормално разпределение около 0.
Това позволява:
-
Картографираме резултатите към персентили, използвайки предполагаемо нормално разпределение.
-
Измерваме интензитета (разстоянието от неутралната стойност) по последователен математически начин.
-
Използваме Fibonacci прагове (0.236, 0.382, 0.618 и т.н.) за класифициране на силата на сентимента.
Това е временно решение, базирано на модел, докато се натрупа достатъчно данни.
Сценарий 2: Достатъчно исторически данни (емпирично разпределение)
След като системата събере достатъчно оценки от новини (напр. 20+, а оптимално 100+), преминаваме към подход, базиран на реални данни, използвайки емпиричното разпределение:
ECDF (Емпирична кумулативна функция на разпределение) показва точно доколко една нова оценка е екстремна или типична в сравнение с всички предишни новинарски стойности.
Този метод:
- Не изисква предположения.
- Адаптира се автоматично към пазарните режими.
- Позволява праговете да се променят динамично въз основа на реални данни за сентимента.
Продължаваме да използваме Фибоначи нивата, но те вече се прилагат върху емпиричната интензивност, а не върху предполагаемо разпределение.
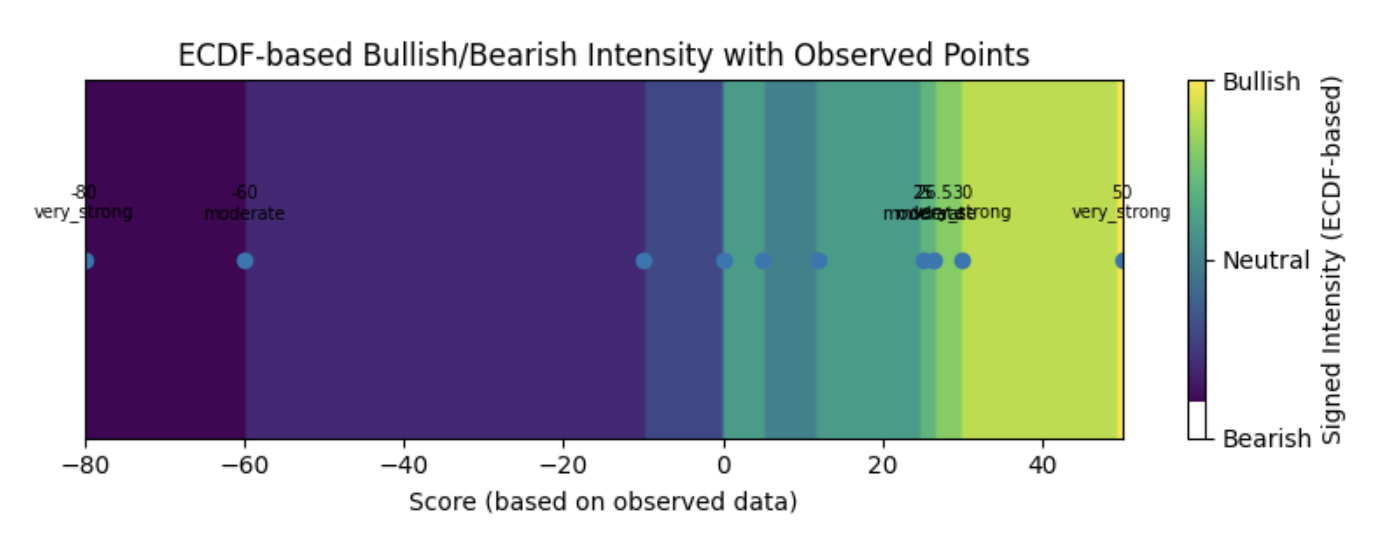
С натрупването на повече новинарски стойности очакваме по-голямата част от тях да попадат в зоните за слаб или умерен сентимент, тъй като екстремните събития са значително по-редки. Това не е предположение, а се научава директно от емпиричното разпределение на данните.
Нов елемент: Класификация на база Фибоначи
За да преведем количествената интензивност в ясни категории (слаб, умерен, силен), използваме нива на Фибоначи като прагове.
Така изграждаме стабилни „лентови зони“ на сентимента, които отразяват силата на новината спрямо общото разпределение на сентимента.
Това е нетрадиционен, но математически обоснован и интуитивен подход, който пасва отлично на нелинейната динамика на крипто пазарите.
Заключение
Чувствителността на крипто пазара към новинарския поток, съчетана с бързото разпространение на информация и човешките поведенчески отклонения, прави суровите ценови данни недостатъчни за реален анализ на сентимента.
Един стабилен модел за сентимент трябва да:
- оценява всички новините в крипто пазара според ясни, структурирани правила,
- нормализира резултата в интерпретируем диапазон,
- и измерва интензивността чрез: предположено нормално разпределение (ранен етап), или емпирично разпределение (зрял етап).
В началната фаза, когато приемаме нормално разпределение, около 95% от всички новинарски оценки трябва да попадат в диапазона „слаб до умерен сентимент“. На по-късен етап, когато моделът натрупа достатъчно реални данни, емпиричното разпределение естествено показва същия модел: екстремните бичи или мечи събития са редки, а повечето новини се групират в средната зона на сентимента.
Този хибриден подход позволява количественият сентимент да се адаптира с натрупването на данни, превръщайки системата в по-точен, основан на данни механизъм за измерване на пазарния сентимент.
Практически пример: J.Labs Sentiment Trend Indicator
За да демонстрираме как работи на практика пълната рамка за сентимент, описана по-горе, прилагаме модела за оценяване върху реален новинарски поток и обобщаваме резултатите в регресионно изгладена сентимент тенденция. Полученият резултат се съпоставя с цената на BTC, за да покаже как информационният натиск се променя във времето.
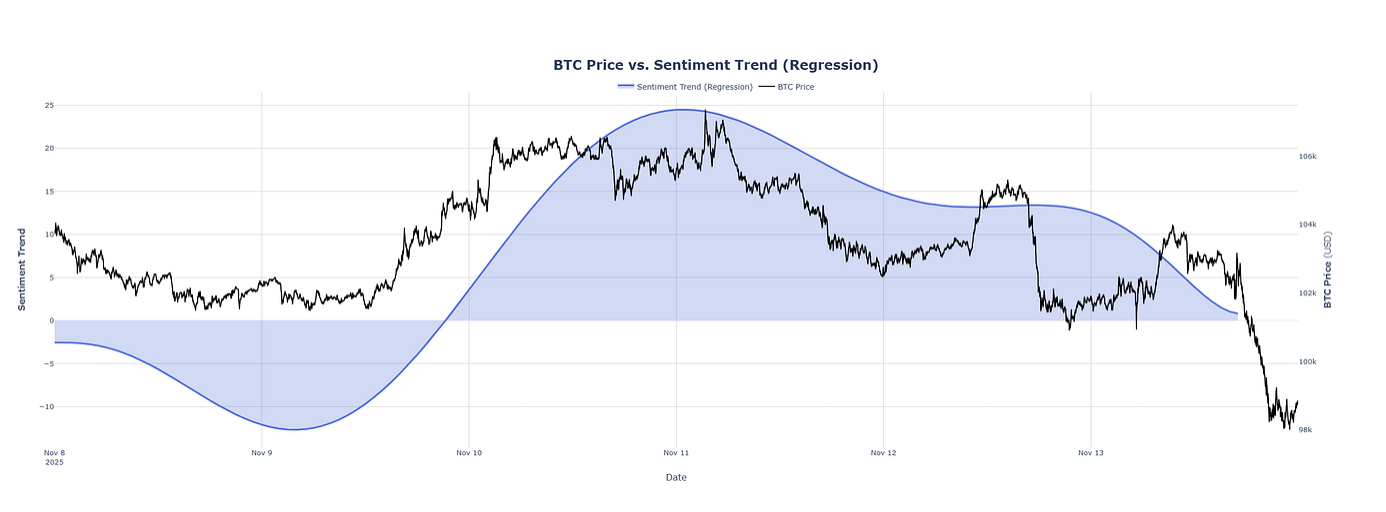
Този индикатор за новините в крипто пазара включва:
- система за оценяване, базирана на правила,
- нормализиране в скала от −100 до +100,
- емпирично мащабиране чрез ECDF (или използване на нормално разпределение в ранните етапи),
- класификация на интензитета на сентимента чрез Фибоначи прагове и
- изглаждане на тренда чрез регресия.
Комбинираният резултат е сентимент крива, която предоставя контекстуален поглед върху информационната среда на пазара и допълва традиционния анализ, базиран само на цената.
Тази визуализация илюстрира как тенденцията на сентимента реагира, когато се обработват нови статии. Позитивният новинарски поток постепенно издига кривата нагоре (бичи сентимент), докато негативните или рисково ориентираните новини я придвижват надолу (мечи сентимент).
Индикаторът за тенденцията на сентимента е също основата на предстоящ продукт за аналитика на сентимента, който подготвяме за пускане. Той ще анализира непрекъснато живи новинарски потоци, ще прилага описаните по-горе методи за оценяване и емпирично мащабиране и ще генерира в реално време прозрения за тенденциите на сентимента за трейдъри, изследователи и институционални потребители. Комбинирайки структурирана логика с динамично моделиране, базирано на данни, системата е проектирана да предоставя точен, прозрачен и обясним поглед върху това как се развива информационният натиск на крипто пазара.
Сценарий 1
def intensity_class(x, sigma=50):
# Compute z-score
z = x / sigma
# Normal CDF
p = norm.cdf(z)
# Symmetric intensity around neutral
I = abs(p - 0.5) / 0.5 # range 0 → 1
# 4. Fibonacci thresholds
if I < 0.236:
label = “Neutral”
elif I < 0.382:
label = “Mild Bullish” if x > 0 else “Mild Bearish”
elif I < 0.618:
label = “Moderate Bullish” if x > 0 else “Moderate Bearish”
else:
label = “Strong Bullish” if x > 0 else “Strong Bearish”
return I, label
intensity, classification = intensity_class(25)
intensity, classification = intensity_class(-25)Когато изчислим стойността на сентимента на новината 25, получаваме:
интензитет: 0.38292492254802624, класификация: Умерено бичи
Същото се получава при изчисление с -25:
интензитет: 0.38292492254802624, класификация: Умерено мечи
Сценарий 2
class SignalScaler:
def __init__(self, window_size=None):
“”“
window_size: if not None, use only last N observations (rolling ECDF).
“”“
self.window_size = window_size
self.values = np.array([])
def fit(self, values):
“”“Initialize with historical scores.”“”
values = np.asarray(values, dtype=float)
self.values = values if self.window_size is None else values[-self.window_size:]
return self
def update(self, x):
“”“Add a new observation and keep window_size if set.”“”
x = float(x)
if self.values.size == 0:
self.values = np.array([x])
else:
self.values = np.append(self.values, x)
if self.window_size is not None and self.values.size > self.window_size:
self.values = self.values[-self.window_size:]
def _ecdf(self, x):
“”“Empirical CDF P(X <= x).”“”
if self.values.size == 0:
return 0.5
return (self.values <= x).mean()
def transform(self, x):
“”“Return percentile, intensity, side and Fibonacci band for x.”“”
x = float(x)
p = self._ecdf(x)
intensity = abs(p - 0.5) / 0.5
# side by value sign
if x > 0:
side = “bullish”
elif x < 0:
side = “bearish”
intensity = intensity
else:
side = “neutral”
signed_intensity = intensity * (1 if side == “bullish”
else -1 if side == “bearish”
else 0)
# Fibonacci-based bands on intensity
I = intensity
if I <= 0.236:
band = “neutral_or_very_mild”
elif I <= 0.382:
band = “mild”
elif I <= 0.618:
band = “moderate”
elif I <= 0.786:
band = “strong”
else:
band = “very_strong”
return {
“value”: x,
“p”: p,
“intensity”: intensity,
“signed_intensity”: signed_intensity,
“side”: side,
“band”: band,
}Example Usage:
‘’‘observed calculated values’‘’
observed_data = [-80, -60, -10, 0, 5, 12, 25, 26.5, 30, 50]
scaler = SignalScaler().fit(observed_data)
‘’‘interpret some example values’‘’
examples = [25, 26.5, 30, 50, -30, -80]
for x in examples:
print(scaler.transform(x))Включили сме метод update() в класа, така че мащабирането да може да се актуализира с всяка новонаблюдавана стойност.
В примера по-долу използваме набор от „observed_data“, за да изградим емпиричното разпределение. След това оценяваме няколко примерни стойности. Резултатите са:
{’value’: 25.0, ‘p’: 0.7, ‘intensity’: 0.399, ‘signed_intensity’: 0.399, ‘side’: ‘bullish’, ‘band’: ‘moderate’}
{’value’: 26.5, ‘p’: 0.8, ‘intensity’: 0.60, ‘signed_intensity’: 0.60, ‘side’: ‘bullish’, ‘band’: ‘moderate’}
{’value’: 30.0, ‘p’: 0.9, ‘intensity’: 0.8, ‘signed_intensity’: 0.8, ‘side’: ‘bullish’, ‘band’: ‘very_strong’}
{’value’: 50.0, ‘p’: 1.0, ‘intensity’: 1.0, ‘signed_intensity’: 1.0, ‘side’: ‘bullish’, ‘band’: ‘very_strong’}
{’value’: -30.0, ‘p’: 0.2, ‘intensity’: 0.6, ‘signed_intensity’: -0.6, ‘side’: ‘bearish’, ‘band’: ‘moderate’}
{’value’: -80.0, ‘p’: 0.1, ‘intensity’: 0.8, ‘signed_intensity’: -0.8, ‘side’: ‘bearish’, ‘band’: ‘very_strong’}При този метод определяме страната (бича или меча) единствено въз основа на знака на резултата спрямо 0.
След това изчисляваме интензитета, използвайки емпиричния персентил (p), и след това го класифицираме в лента на настроенията, използвайки прагове, базирани на Фибоначи.