Степенен показател на Хърст като статистически тест за връщане към средната стойност във финансови времеви редове

Преди разработването на каквато и да е печеливша стратегия за търговия, прогнозиране или обработка на сигнали, анализаторът трябва да установи фундаменталната природа на данните: дали времевият ред е самокоригиращ се (mean reverting), напълно случаен (random walk) или притежава инерция (trending). Показател на Хърст (H), наречен на британския хидролог Харолд Едуин Хърст, е статистическа формула, използвана за измерване на „дългосрочната памет“ на данните. Той е незаменим инструмент за трейдъри и изследователи, фокусирани върху разработването на стратегии за връщане към средната стойност.

Важно е да се отбележи, че Hurst експонентът измерва дългосрочна зависимост, а не краткосрочна автокорелация, и не представлява директен сигнал за вход.

1. Дефиниция и математическа основа

Показател на Хърст се определя чрез асимптотичното поведение на т.нар. рестандартизиран обхват (rescaled range) като функция от времевия период на наблюдение. Математическата зависимост следва „степенен закон“ (power law):

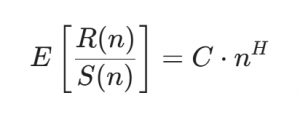
Където:

• E[x]: Очакваната стойност на статистиката.
• R(n): Размахът (обхватът) на първите n кумулативни отклонения от средната стойност.
• S(n): Стандартното отклонение на първите n стойности от серията.
• n: Броят на наблюденията за времеви прозорец x.
• C: Константа.
• H: Търсеният показател на Хърст.

В практиката H се изчислява чрез логаритмуване на двете страни на уравнението:

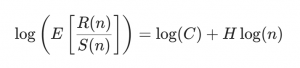
За различни дължини на прозореца n изчисляваме R(n) / S(n) и усредняваме за дадения n. След това правим логаритмична трансформация.

Това означава, че ако дефинираме:
X = log(n)

Y = log(E [ R(n) / S(n) ])

То между X иY има приблизително линейна зависимост.

Ако начертаем точките X и Y за всички избрани n, можем да напаснем линейна регресия, а именно:
Y = a + bX

Тогава b = H, което по същество е наклона на правата.

2. Интерпретация на резултата

Стойността на Хърст експонентата (H) варира в интервала (0, 1) и позволява класифициране на поведението на даден финансов актив в три основни пазарни режима:

• H < 0.5: Анти-персистентност (Mean Reversion)

При стойности на H под 0.5 времевият ред демонстрира анти-персистентно поведение, характеризиращо се с отрицателна дългосрочна автокорелация. Това означава, че ценовите движения имат тенденция да се компенсират във времето — покачванията по-често са последвани от спадове и обратно.

Такъв пазарен режим е типичен за mean-reverting процеси, при които цената се колебае около дългосрочна равновесна стойност. Пазарът може да бъде описан като „самокоригиращ се“, без устойчива посока на движение.

• H = 0.5: Случайно блуждаене (Random Walk)

Стойност H ≈ 0.5 индикира, че времевият ред следва случайно блуждаене, при което липсва дългосрочна памет. Движенията на цената са статистически независими едно от друго и не съдържат предсказуема структура.

В този режим ценовият процес често се моделира чрез Броуново движение, което е в основата на класическите финансови модели, включително хипотезата за ефективния пазар. Информацията за миналото поведение на цената не носи полезна информация за бъдещите ѝ движения.

• H > 0.5: Персистентност (Trending)

Когато H е по-голямо от 0.5, времевият ред проявява персистентност, характеризираща се с положителна дългосрочна автокорелация. В този режим ценовите движения имат тенденция да се запазват във времето — възходящите трендове по-често продължават, отколкото се обръщат, и обратно.

Това поведение е типично за трендови пазари, при които цената демонстрира инерция и устойчива посока на движение, често асоциирана с momentum ефекти.

3. Mean Reversion и приложение във финансите

Теорията за връщане към средната стойност (Mean Reversion) предполага, че при определени пазарни условия финансови променливи като цени на акции или валутни курсове проявяват тенденция да се връщат към своята дългосрочна средна стойност след екстремни отклонения. В този контекст Hurst експонентата служи като статистически филтър за идентифициране на mean-reverting режими във времевите редове.

• Идентифициране на възможности:
  Ако изчислим, че акции на компания X имат H = 0.35, това индикира силно анти-персистентно поведение. Значителните отклонения от средната цена са по-скоро временни и създават потенциал за стратегии, базирани на mean reversion, при които се търси експлоатация на отклоненията от равновесното ниво.
• Дългосрочна памет:
  За разлика от процеси, наподобяващи „бял шум“, при които миналото няма информативна стойност, ниските стойности на Hurst експонентата отразяват наличие на дългосрочна зависимост. Миналите ценови движения влияят статистически върху бъдещото поведение на процеса, което позволява моделиране на механизма на самокорекция.
• Примери за консистентни стратегии:

• • Pairs Trading:
    Hurst експонентата може да се използва за предварителен анализ на ценовия спред между два актива. Спред с H < 0.5 индикира mean-reverting поведение, което е необходимо (но не достатъчно) условие за прилагане на стратегии тип pairs trading.

  • Статистически арбитраж:
    Чрез анализ на инструменти с ниски стойности на Hurst експонентата, анализаторите могат да идентифицират статистически равновесни състояния, които пазарът временно е нарушил, и да изграждат стратегии за тяхното постепенно възстановяване.

4. Практическа реализация: Python скрипт за изчисляване на Hurst Exponent

За практическо приложение използваме готови статистически библиотеки в Python. Следният клас позволява изчисление на Hurst Exponent и класификация на пазарния режим:

import numpy as np
import pandas as pd
import nolds
from scipy import stats


class MarketRegimeDetector:
    """
    High-level market regime detection using
    established statistical libraries.
    """

    def __init__(self, returns, significance_level=0.05):
        self.returns = returns.dropna()
        self.alpha = significance_level

    def estimate_hurst(self):
        """Estimates the Hurst Exponent using R/S method."""
        hurst_value = nolds.hurst_rs(self.returns.values)
        return hurst_value

    def classify_market(self, hurst_value):
        """Classifies market behavior based on Hurst Exponent."""
        if hurst_value < 0.45:
            return "Mean Reverting"
        elif hurst_value > 0.55:
            return "Trending"
        else:
            return "Random Walk"
    def analyze(self):
        hurst = self.estimate_hurst()
        regime = self.classify_market(hurst)
        return {"hurst_exponent": hurst, "market_regime": regime}

Описание:

• estimate_hurst() изчислява Hurst Exponent чрез стандартизирана R/S процедура (nolds).
  
• classify_market() класифицира пазара като Mean Reverting, Trending или Random Walk.
  
• analyze() комбинира резултатите за цялостен анализ на пазарния режим.

Заключение

Показателят на Хърст предлага математически обоснован подход за определяне на потенциала за връщане към средната стойност. Независимо дали изграждате алгоритмичен модел или анализирате пазарната динамика, включването на този анализ предлага дълбоко разбиране за характеристиките на данните. Добре проектираната стратегия, базирана на Hurst Exponent и подкрепена от статистическа проверка, може да бъде източник на постоянна доходност в един иначе хаотичен пазар.